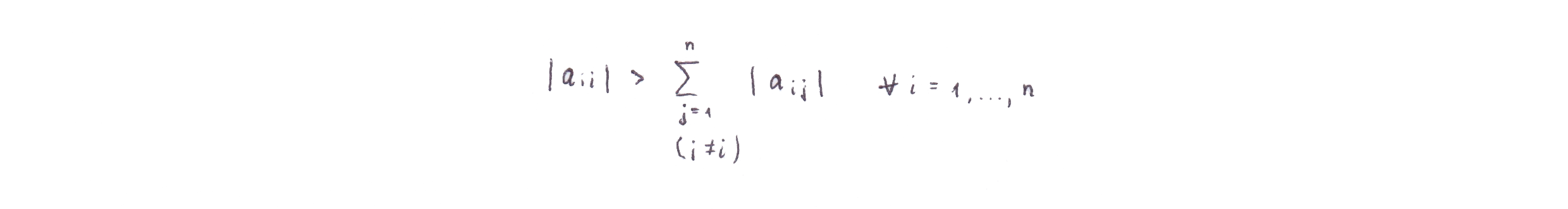Метод Якоби
Представим матрицу коэффициентов в виде
где - диагональная, а и - соответственно левая и правая строго треугольные матрицы (т.е. на главной диагонали вместо вектора D будут стоять нули).
 Тогда система может быть записана в виде
приедем уравнение вида к виду
где в последнем уравнении ,
Основанный на таком приведении уравнения вида к виду метод простых итераций называют методом Якоби.
В векторно-матричных обозначениях, он определяется формулой.
Тогда система может быть записана в виде
приедем уравнение вида к виду
где в последнем уравнении ,
Основанный на таком приведении уравнения вида к виду метод простых итераций называют методом Якоби.
В векторно-матричных обозначениях, он определяется формулой.
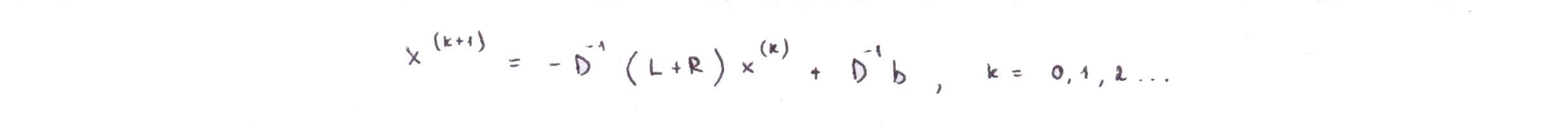 Выведем формулу для итерационных вычислений
Заметим, что обратной матрицей к матрице служит матрица с элементами диагонали , поэтому система в раскрытом виде будет равнозначна выражению диагональных элементов через остальные
Выведем формулу для итерационных вычислений
Заметим, что обратной матрицей к матрице служит матрица с элементами диагонали , поэтому система в раскрытом виде будет равнозначна выражению диагональных элементов через остальные
 Для записи итерациооного процесса, добавим к системе индексы, показывающие текущую итерацию.
Для записи итерациооного процесса, добавим к системе индексы, показывающие текущую итерацию.

Теорема. В случае диагонального преобладания в матрице метод Якоби сходится. Определение. Диагональное преобладание в матрице означает, что