Пусть в уравнении $Ax = b$ матрица коэффициентов имеет следующий вид приведем ее к треугольному виду с помощью прямого хода метода Гаусса Обратим внимание на относительную величину коэффициентов в последнем столбце. В случае $n\times{}n$ матрицы похожего типа прямой ход метода Гаусса допускает рост элементов до величины $2^{n-1}$. При больших $n$ это может привести к возникновению погрешностей округлений, причем в данной ситуации постолбцовый выбор главного элемента не даст эффекта. Метод вращений учитывает проблему, рассмторенную в примере, давая точный результат при работе с матрицами подобного вида.

Рассмотрим систему линейных уравнений вида

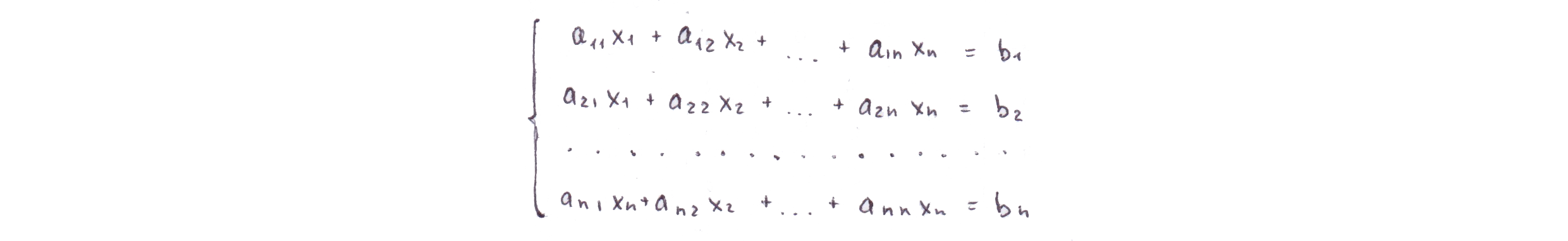
Метод вращений, как и метод Гаусса, состоит из прямого хода и обратного. Цель прямого хода остается неизменной - последовательное исключение неизвестных и, как следствие, приведение матрицы к треугольному виду. Делается это следующим образом. Пусть $с_1$ и $s_1$ - некоторые отличные от нуля числа. Умножим первое уравнение системы на $с_1$, второе - на $s_1$ и сложим их. Полученным уравнением заменим первое уравнение системы. Затем первое уравнение исходной системы умножим на $-s_1$, а второе - на $c_1$ и результатом их сложения заменяем второе уравнение исходной системы. Таким образом, первые два уравнения системы заменяются следующими уравнениями На введенные параметры $с_1$ и $s_1$ накладываются два условия

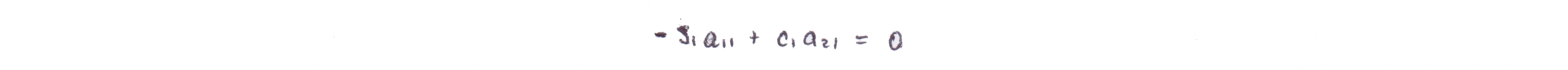
• условие, обеспечивающие исключение $x_1$ из второго уравнения

• условие нормировки Исходя из этих двух условий, коэффициенты рассчитываются по следующим формулам 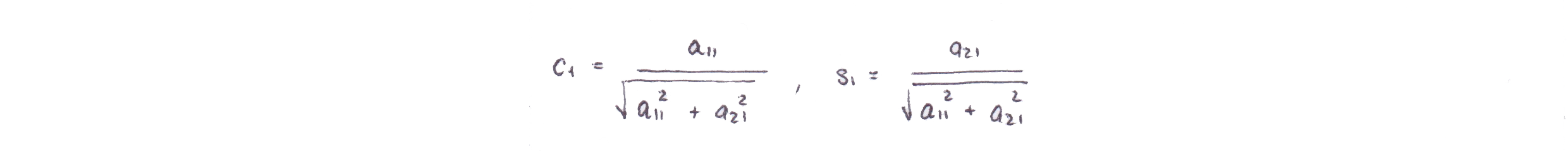Заметим, что коэффициенты возможно интерпретировать как синус и косинус некоторого угла $\alpha$. Таким образом, каждый шаг прямого хода будет поворачивать (?) ... в плоскости, определяемой индексами ... В результате преобразований получится матрица 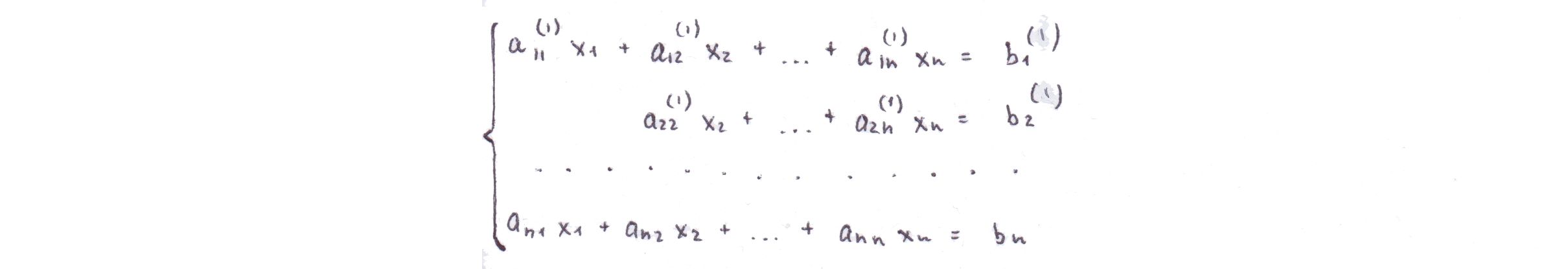где 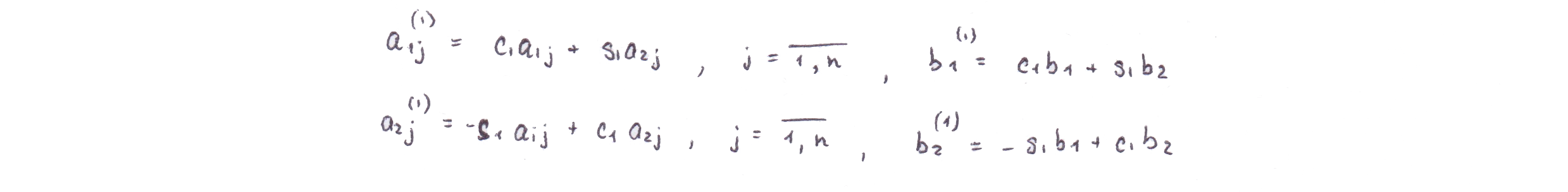Далее исключаем $x_1$ из третьей строчки. Первое уравнение системы заменяется новым, полученным сложением результатов умножения первого и третьего уравнений полученной системы соответственно на третье уравнение системы заменяется на уравнение, полученным сложением результатов умножения тех же уравнений на соответственно на $-s_2$ и $c_1$ Получаем систему где Проделав такие преобразования $n-1$ раз, исключим $x_1$ из 2-го, 3-го ... n-го уравнений. Система примет вид 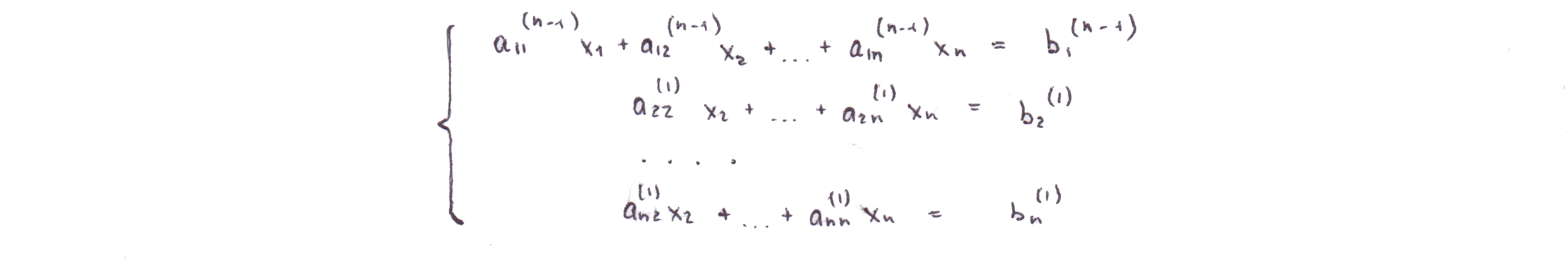Полученная система обладает важным свойством: длина любого вектора-столбца (в n-мерном пространстве, где n - количество строк матрицы) расширенной матрицы системы остается такой же, как и у соответствующего столбца исходной системы. Доказывается это следующим образом таким образом, сумма квадратов пары элементов любого столбца, изменяемых на одном шаге прямого хода, остается неизменным. Так как остальные элементы столбцов остаются неизменными, то, значит, на любом этапе преобразований длина вектора будет сохраняться. Далее за $n-2$ шага преобразуем систему добиваясь обнуления всех элементов под $a_{22}^{(1)}$ После $n-1$ этапов прямого хода система будет преобразована в треугольный вид Для нахождения неизвестных из полученной системы используется обратный ход, аналогичный методу Гаусса.

Реализация

from matrix_np_api import *


def solve_with_rotation(m):
    """Solve system with rotation method.
    :param m: numpy matrix
    :return: None
    """
    n = m.shape[0]
    # forward trace
    for i in range(n-1):
        for j in range(i + 1, n):
            c = m[i, i] / (m[i, i]**2 + m[j, i]**2) ** .5
            s = m[j, i] / (m[i, i]**2 + m[j, i]**2) ** .5
            tmp1 = m[i, :] * c + m[j, :] * s
            tmp2 = m[i, :] * -s + m[j, :] * c
            m[i, :] = tmp1
            m[j, :] = tmp2

    # check for non-singularity
    if is_singular(m):
        print('The system has infinite number of answers...')
        return

    # backward trace
    x = np.matrix([0.0 for i in range(n)]).T
    for k in range(n - 1, -1, -1):
        x[k, 0] = (m[k, -1] - m[k, k:n] * x[k:n, 0]) / m[k, k]

    # Display results
    display_results(x)


def is_singular(m):
    """Check matrix for nonsingularity.
    :param m: matrix (list of lists)
    :return: True if system is nonsingular
    """
    return np.any(np.diag(m) == 0)

m = read_matrix('rotation_matrix.txt')
solve_with_rotation(m)