LU разложение

Пусть $A = (a_{ij})^{n}_{i,j=1}$ - данная $n\times n$ матрица, а $L = (l_{ij})^{n}_{i,j=1}$ и $U = (u_{ij})^{n}_{i,j=1}$- соотвественно нижняя (левая) и верхняя (правая) треугольные матрицы.

Теорема. Если все главные миноры квадратной матрицы $A$ отличны от нуля, то существуют такие нижняя $L$ и верхняя $U$ треугольные матрицы, что $A = LU$. Если элементы диагонали одной из матриц $L$ или $U$ фиксированы (ненулевые), то такое разложение единственно.

Ниже рассматриваются формулы для фактического разложения матриц в случае фиксирования диагонали нижней треугольной матрицы $L$. Найдем $l_{ij}$ (при i>j) и $u_{ij}$ (при i <= j) такие, что

После перемножения матриц получим следующую систему

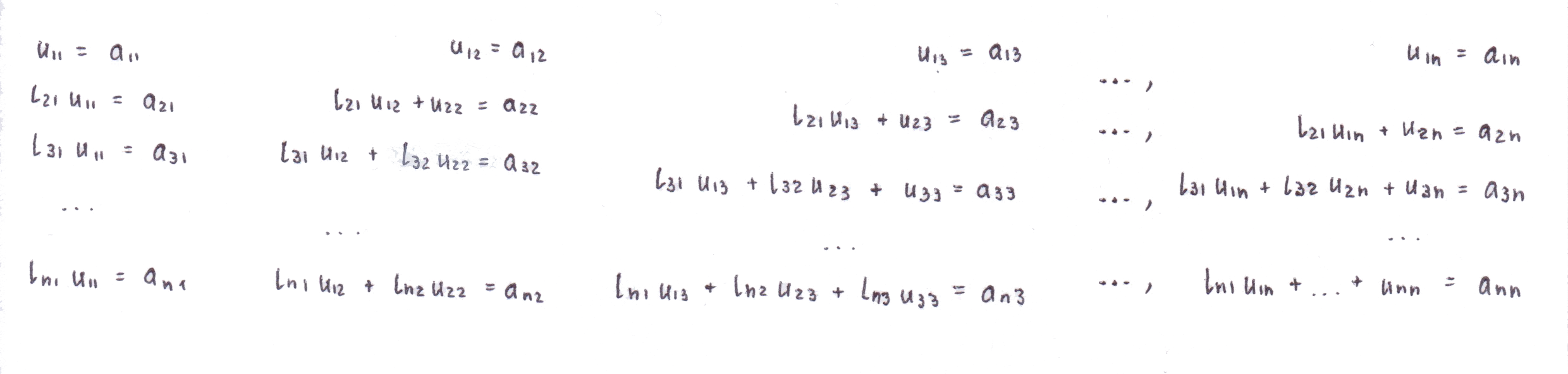Эта система позволяет находить неизвестные $u_{ij}$ и $l_{ij}$ в следующем порядке. Из первой строки уравнений имеем из оставшейся части первого столбца имеем 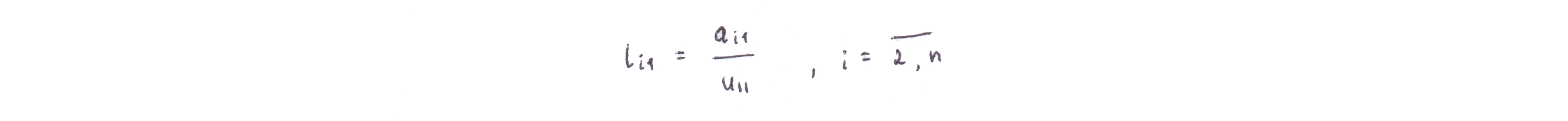из оставшейся части второй строки имеем из оставшейся части второго столбца имеем 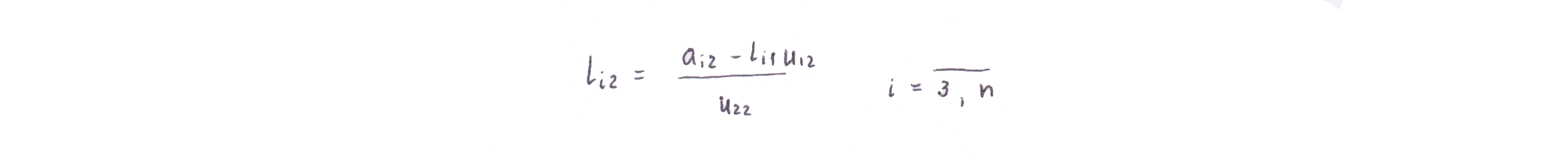и т.д. Обобщая, все элементы матрицы неизвестных могут быть получены по формулам

NB Вычисления матрицы неизвестных img удобно проводить, ориентируясь на двумерный массив для хранения LU-разложения в памяти компьютера.

NB Препятствием в решении описанного процесса LU-раложения может оказаться равенство нулю диагональных элементов матрицы $U$, поскольку на них будет выполняться деление. Отсюда требование теоремы, приведённой выше. Вместо проверки на равенство нулю главных миноров матрицы удобнее сделать проверку для элементов $u_{ij}$ в процессе их вычисления.

Решение СЛАУ с помощью LU разложения

После разложения матрицы $A$ в две треугольные $L$ и $U$, вместо уравнения $Ax = b$ можно записать уравнение $LUx = b$ Введя вспомогательный вектор $y = (y_1, y_2, ... , y_n)^{T}$, последнее равенство можно записать в виде системы $\begin{cases} Ly = b, \\ Ux = y \end{cases}$ Исходя из приведенной системы, необходимо решить две системы с трегольными матрицами коэффициентов. Рассматривая первое уравнение, получим формулы для вычисления вспомогательного вектора 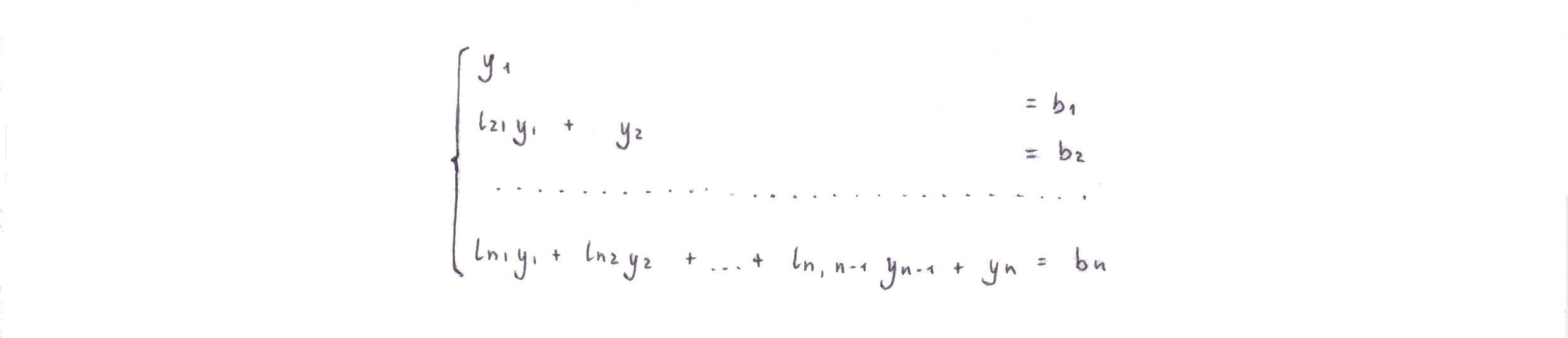$y$. Все $y_i$ могут быть последовательно найдены по формуле 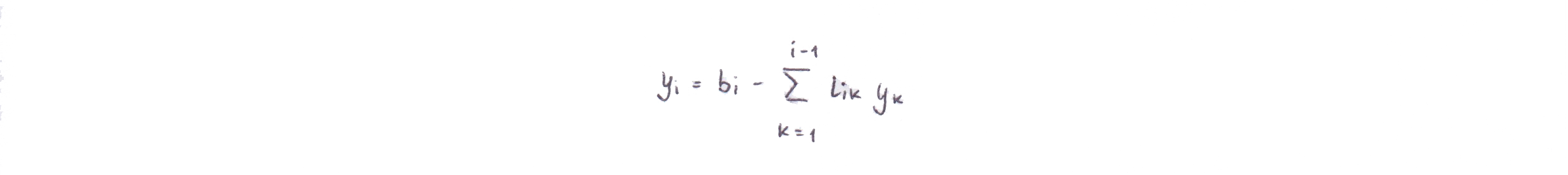Рассмотрим второе уравнение системы Отсюда значения неизвестных находятся в обратном порядке по формуле

Вычисление определителя

Вычисление определителя LU-факторизованной матрицы $A$ опирается на свойство определителя произведения матриц и сводится к перемножению $n$ чисел

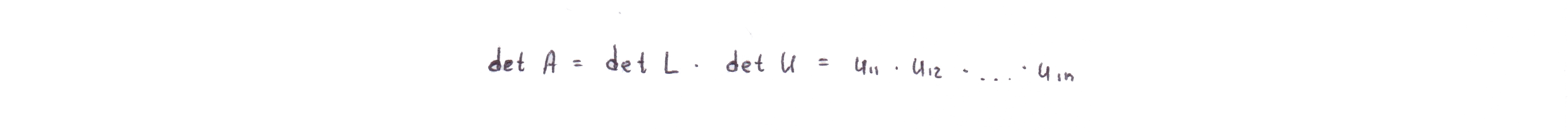
Обращение систем с помощью LU разложения

Ниже выводятся формулы для выражения элементов обратной матрицы через элементы матриц $L$ и $U$. Пусть матрицы $A$ и $U$ обратимы (матрица $L$ обратима всегда). Тогда Унможим последнее равенство поочередно на $U$ слева и на $L$ справа Обозначим искомые элементы матрицы $A^{-1}$ через $x_{ij}$. Учитывая, что треугольные матрицы при обращении сохраняют свою структуру, перепишем равенства в следующем виде Звездочкой обозначены некоторые числа, знание которых для нахождения обратной матрицы не требуется. Полученные матричные неравенства можно рассматривать как систему уравнений с $2n^2$ неизвестными $x_{ij}$. Из этих $2n^2$ уравнений $n^2$ имеют известные правые части (0 или 1). Соотвествующая им матрица уравнений приведена ниже Обобщая, можно вывести три типа связей 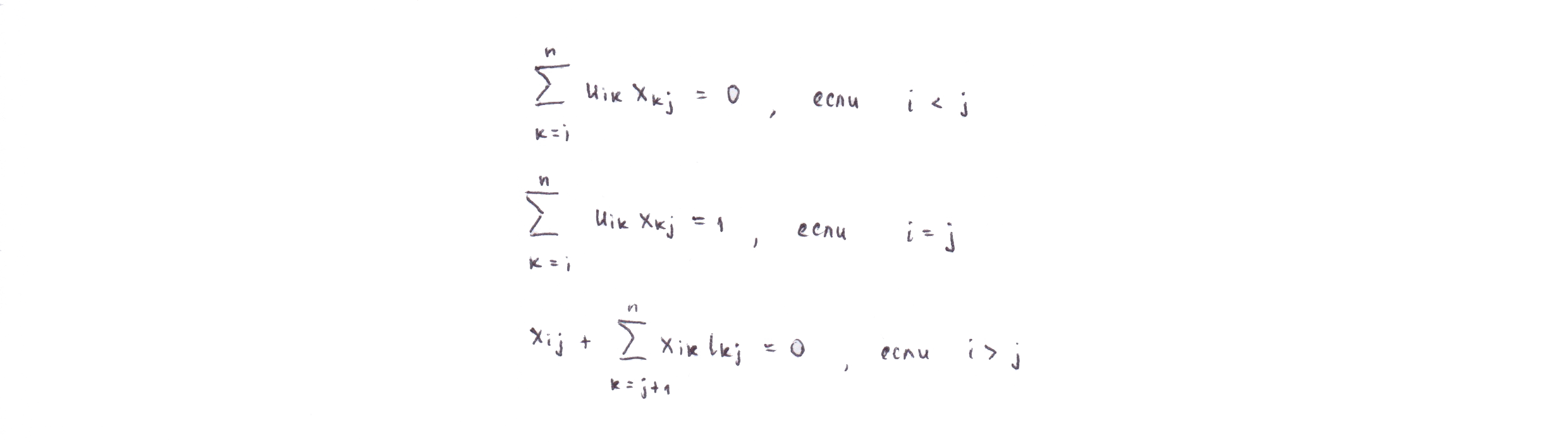Из полученных формул выразим коэффициенты обратной матрицы 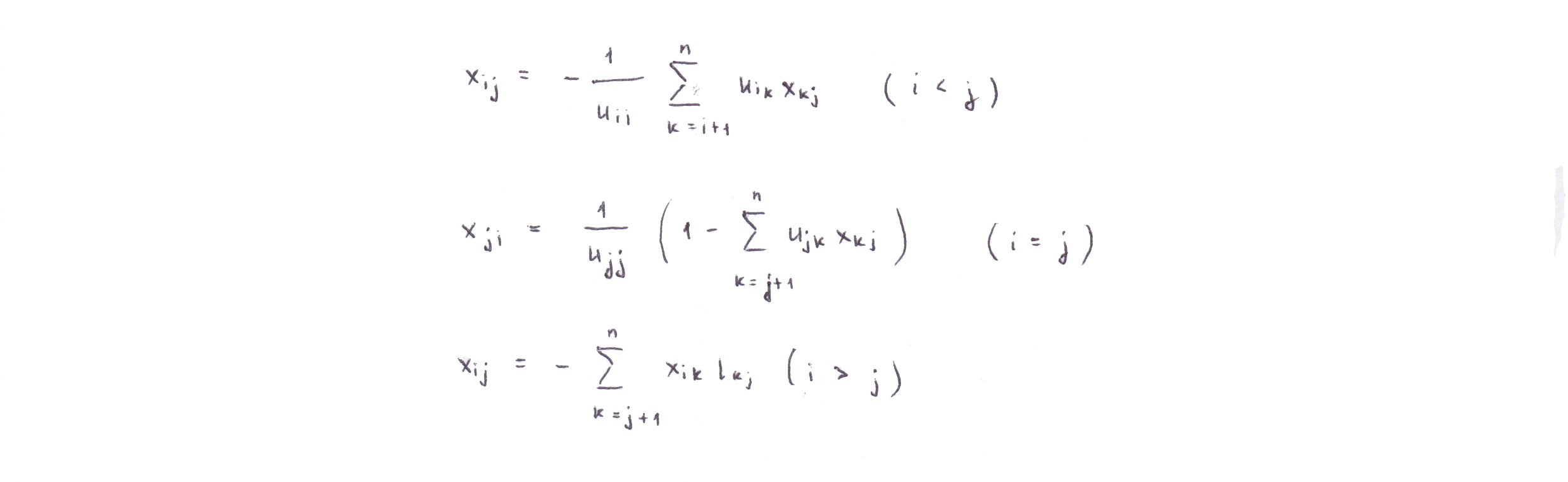Полученные формулы позволяют эффективно обращать LU-факторизованную матрицу, пользуясь следующим порядком вычисления: (числа рядом со стрелочками обозначают шаг вычислений) здесь на шагах 1, 4, ... необоходимо использовать формулу 1. На 2, 5 ... - формулу 2. На 3, 6 ... - формулу 3.

Релизация

Реализуем функцию LU-разложения матрицы коэффициентов

def decompose_to_LU(a):
    """Decompose matrix of coefficients to L and U matrices.
     L and U triangular matrices will be represented in a single nxn matrix.
    :param a: numpy matrix of coefficients
    :return: numpy LU matrix
    """
    # create emtpy LU-matrix
    lu_matrix = np.matrix(np.zeros([a.shape[0], a.shape[1]]))
    n = a.shape[0]

    for k in range(n):
        # calculate all residual k-row elements
        for j in range(k, n):
            lu_matrix[k, j] = a[k, j] - lu_matrix[k, :k] * lu_matrix[:k, j]
        # calculate all residual k-column elemetns
        for i in range(k + 1, n):
            lu_matrix[i, k] = (a[i, k] - lu_matrix[i, : k] * lu_matrix[: k, k]) / lu_matrix[k, k]

    return lu_matrix

Реализуем вспомогательные функции получения треугольных L и U матриц из одной LU матрицы.

def get_L(m):
    """Get triangular L matrix from a single LU-matrix
    :param m: numpy LU-matrix
    :return: numpy triangular L matrix
    """
    L = m.copy()
    for i in range(L.shape[0]):
            L[i, i] = 1
            L[i, i+1 :] = 0
    return np.matrix(L)


def get_U(m):
    """Get triangular U matrix from a single LU-matrix
    :param m: numpy LU-matrix
    :return: numpy triangular U matrix
    """
    U = m.copy()
    for i in range(1, U.shape[0]):
        U[i, :i] = 0
    return U

Для проверки правильности разложения, перемножим матрицы L и U и сравним с исходной матрицей коэффициентов

a, b = read_matrix_a_b('data/lu_matrix.txt')
display_matrix(a)

LU = decompose_to_LU(a)
L = get_L(LU)
U = get_U(LU)

display_matrix(L * U)

Напишем функцию для решения системы уравнений, исходя из полученного LU-разложения

def solve_LU(lu_matrix, b):
    """Solve system of equations from given LU-matrix and vector b of absolute terms.
    :param lu_matrix: numpy LU-matrix
    :param b: numpy matrix of absolute terms [n x 1]
    :return: numpy matrix of answers [n x 1]
    """
    # get supporting vector y
    y = np.matrix(np.zeros([lu_matrix.shape[0], 1]))
    for i in range(y.shape[0]):
        y[i, 0] = b[i, 0] - lu_matrix[i, :i] * y[:i]

    # get vector of answers x
    x = np.matrix(np.zeros([lu_matrix.shape[0], 1]))
    for i in range(1, x.shape[0] + 1):
        x[-i, 0] = (y[-i] - lu_matrix[-i, -i:] * x[-i:, 0] )/ lu_matrix[-i, -i]

    return x