Метод Гаусса является наиболее известным методом решения систем линейных уравнений. Суть метода заключается в последовательном исключении неизвестных. Ниже выводится совокупность формул, позволяющих в итоге получить значения неизвестных. Метод Гаусса состоит из двух этапов - прямого хода и обратного хода.
Рассмотрим систему линейных уравнений вида
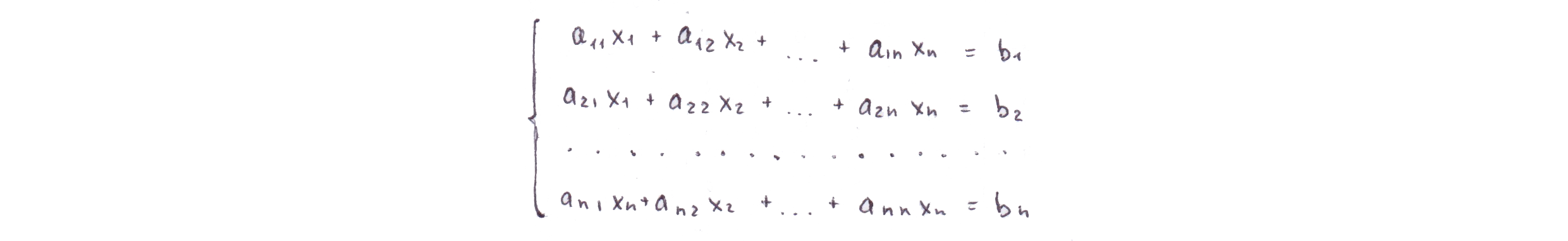 Прямой ход
Прямой ход
Задача прямого хода заключается в приведении системы к треугольному виду. Первый шаг - исключим из второго, третьего, ..., n-го уравнений. Второй шаг - исключим из третьего, четвертого, ..., n-го уравнений и т.д.
Результатом первого шага будет система
 коэффициенты с верхним индексом 1 (верхний индекс показывает номер шага) подсчитываются по формулам
коэффициенты с верхним индексом 1 (верхний индекс показывает номер шага) подсчитываются по формулам
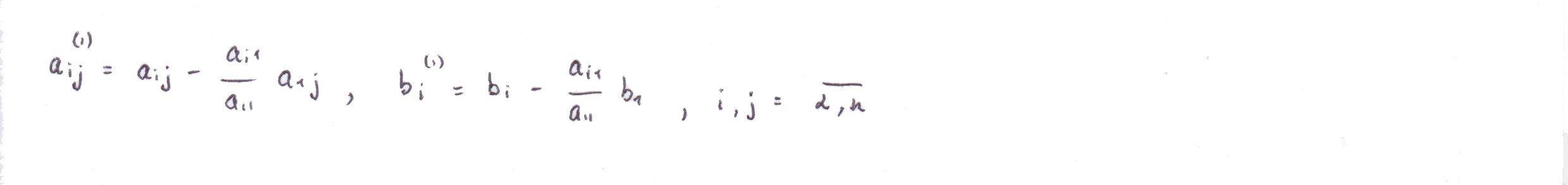 Результатом второго шага будет система
Результатом второго шага будет система
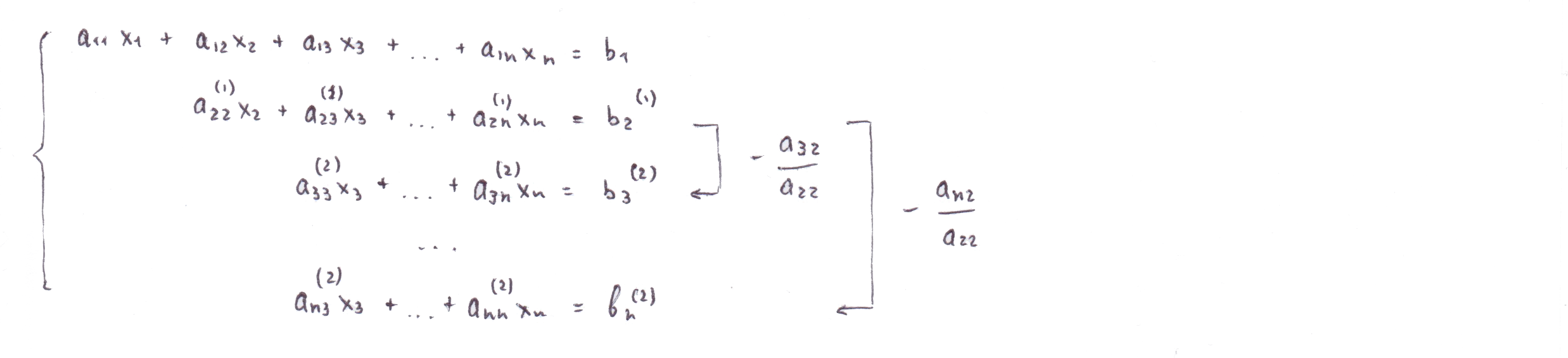 Заметим, что коэффициенты для второго шага вычисляются по формулам
Заметим, что коэффициенты для второго шага вычисляются по формулам
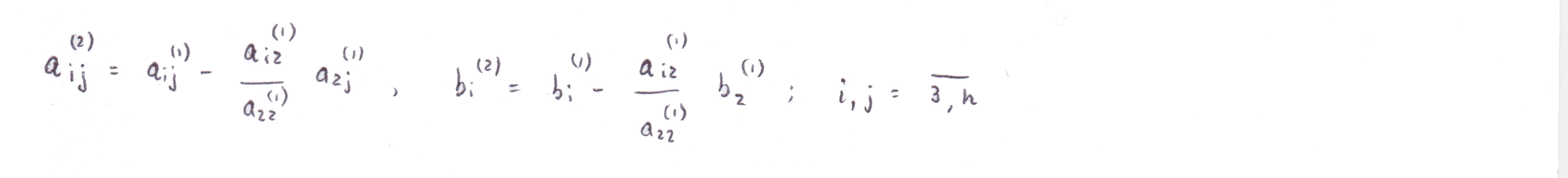 Продолжая процесс на (n-1) шаге система приобретает треугольный вид
Продолжая процесс на (n-1) шаге система приобретает треугольный вид
 Коэффициенты этой системы могут быть получены с помощью формул общего вида:
Коэффициенты этой системы могут быть получены с помощью формул общего вида:
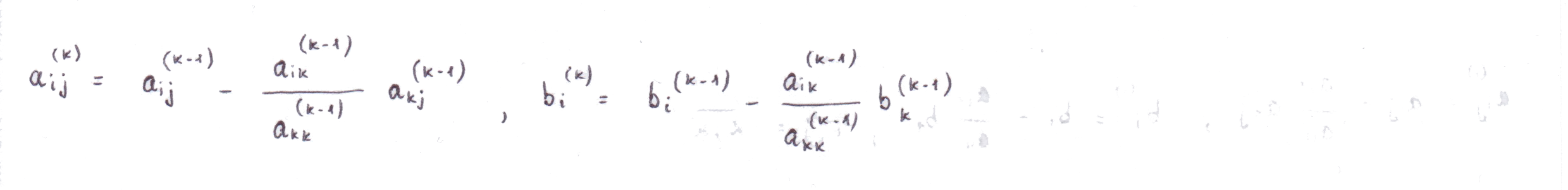
Обратный ход
Заключается в вычислении неизвестных, начиная с последнего и двигаясь вверх.
Для нахождения вычислим простую дробь
 Для нахождения
Для нахождения
 Для первых неизвестных формулы принимают следующий вид
Для первых неизвестных формулы принимают следующий вид
 Исходя из вышеприведенных уравнений возможно сфомулировать общую формулу обратного хода
Исходя из вышеприведенных уравнений возможно сфомулировать общую формулу обратного хода
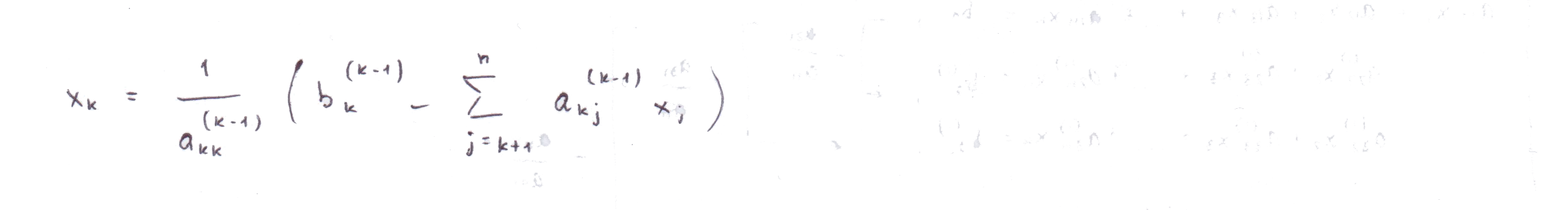
Постолбцовый выбор главных элементов
Так как реальные машинные вычисления производятся с усеченными числами, неизбежны ошибки округления. Если на каком-то этапе знаменатели дробей окажуться слишком маленькими, выполнение алгоритма может привести к неверным результатам. Рассмотрим пример
Вычтем из второй строчки первую, умноженную на
Подставляя в первую строчку
Подставляя во вторую строчку найденные и имеем
Решим ту же систему, поменяв местами строчки в исходной системе
Подставляя полученные значения в систему, получаем результат, более приблеженный к реальности, чем результат из предыдущего решения.
Чтобы уменьшить влияние ошибок округления и исключить деление на нуль на каждом этапе прямого хода, уравнения системы решено переставлять так, чтобы деление проводилось на наибольший по модулю в данном столбце элемент (что было сделано во втором варианте решения). Это делается с целью избежания ситуаций, когда близко к нулю. Если это так, то результатом деления на оказатся большое число с большой абсолютной погрешностью.
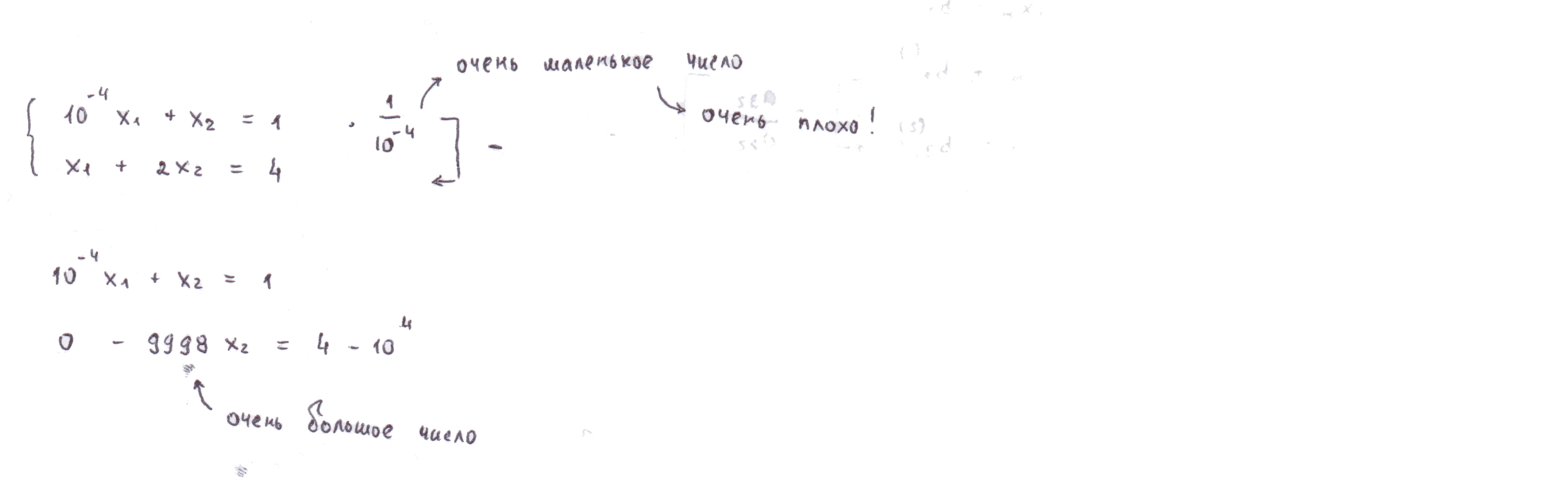 Числа, на которые производится деление в методе Гаусса, называются ведущими или главными элементами.
Таким образом, в начале каждого этапа прямого хода решения системы следует добавить логику перестановки строк для выполнения приведенного условия.
Числа, на которые производится деление в методе Гаусса, называются ведущими или главными элементами.
Таким образом, в начале каждого этапа прямого хода решения системы следует добавить логику перестановки строк для выполнения приведенного условия.
Реализация
from matrix_api import *
def bubble_max_row(m, col):
"""Replace m[col] row with the one of the underlying rows with the modulo greatest first element.
:param m: matrix (list of lists)
:param col: index of the column/row from which underlying search will be launched
:return: None. Function changes the matrix structure.
"""
max_element = m[col][col]
max_row = col
for i in range(col + 1, len(m)):
if abs(m[i][col]) > abs(max_element):
max_element = m[i][col]
max_row = i
if max_row != col:
m[col], m[max_row] = m[max_row], m[col]
def solve_gauss(m):
"""Solve linear equations system with gaussian method.
:param m: matrix (list of lists)
:return: None
"""
n = len(m)
# forward trace
for k in range(n - 1):
bubble_max_row(m, k)
for i in range(k + 1, n):
div = m[i][k] / m[k][k]
m[i][-1] -= div * m[k][-1]
for j in range(k, n):
m[i][j] -= div * m[k][j]
# check modified system for nonsingularity
if is_singular(m):
print('The system has infinite number of answers...')
return
# backward trace
x = [0 for i in range(n)]
for k in range(n - 1, -1, -1):
x[k] = (m[k][-1] - sum([m[k][j] * x[j] for j in range(k + 1, n)])) / m[k][k]
# Display results
display_results(x)
def is_singular(m):
"""Check matrix for nonsingularity.
:param m: matrix (list of lists)
:return: True if system is nonsingular
"""
for i in range(len(m)):
if not m[i][i]:
return True
return False
m = read_matrix('matrix10x10.txt')
solve_gauss(m)
Векторная реализация
Рассматривается реализация с использованием векотрых операций при помощи библиотеки numpy
import numpy as np
from matrix_np_api import *
def bubble_max_row(m, k):
"""Replace m[col] row with the one of the underlying rows with the modulo greatest first element.
:param m: numpy matrix
:param k: number of the step in forward trace
:return: None. Function changes the matrix structure.
"""
ind = k + np.argmax(np.abs(m[k:, k]))
if ind != k:
m[k, :], m[ind, :] = np.copy(m[ind, :]), np.copy(m[k, :])
def solve_gauss(m):
"""Solve linear equations system with gaussian method.
:param m: numpy matrix
:return: None
"""
n = m.shape[0]
# forward trace
for k in range(n - 1):
bubble_max_row(m, k)
for i in range(k + 1, n):
# modify row
frac = m[i, k] / m[k, k]
m[i, :] -= m[k, :] * frac
# check modified system for nonsingularity
if is_singular(m):
print('The system has infinite number of answers...')
return
# backward trace
x = np.matrix([0.0 for i in range(n)]).T
for k in range(n - 1, -1, -1):
x[k, 0] = (m[k, -1] - m[k, k:n] * x[k:n, 0]) / m[k, k]
# Display results
display_results(x)
def is_singular(m):
"""Check matrix for nonsingularity.
:param m: matrix (list of lists)
:return: True if system is nonsingular
"""
return np.any(np.diag(m) == 0)
m = read_matrix('matrix10x10.txt')
solve_gauss(m)